|
Connections within the group of differentiated gamma functions and with other function groups
Representations through more general functions
The differentiated gamma functions  , , 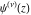 , , 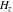 , and , and 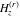 are particular cases of the more general hypergeometric and Meijer G functions. Although the arguments of these functions do not depend on the variable are particular cases of the more general hypergeometric and Meijer G functions. Although the arguments of these functions do not depend on the variable 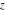 , it is included in their parameters. , it is included in their parameters.
For example, 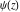 , ,  , , 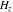 , and , and 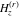 can be represented through generalized hypergeometric functions can be represented through generalized hypergeometric functions 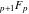 by the following formulas: by the following formulas:
The aforementioned general formulas can be rewritten using the classical Meijer G functions as follows:
Representations through related equivalent functions
The differentiated gamma functions 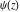 , , 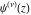 , , 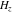 , and , and 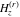 can be represented through derivatives of the gamma function can be represented through derivatives of the gamma function 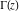 : :
The differentiated gamma functions 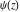 , , 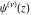 , , 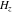 , and , and 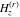 can also be represented through derivatives of the logarithm of the gamma function can also be represented through derivatives of the logarithm of the gamma function 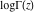 : :
The functions 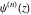 and and 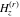 are intimately related to the Hurwitz zeta function are intimately related to the Hurwitz zeta function 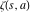 and the Bernoulli polynomials and numbers and the Bernoulli polynomials and numbers  , , 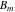 by the formulas: by the formulas:
Representations through other differentiated gamma functions
The differentiated gamma functions 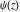 , , 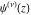 , , 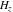 , and , and 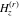 are interconnected through the following formulas: are interconnected through the following formulas:
|