|
The rounding and congruence functions include seven basic functions. They all deal with the separation of integer or fractional parts from real and complex numbers: the floor function (entire part function)  , the nearest integer function (round) , the nearest integer function (round) 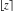 , the ceiling function (least integer) , the ceiling function (least integer) 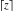 , the integer part , the integer part 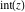 , the fractional part , the fractional part 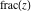 , the modulo function (congruence) , the modulo function (congruence) 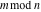 , and the integer part of the quotient (quotient or integer division) , and the integer part of the quotient (quotient or integer division) 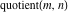 . .
The floor function (entire function) 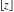 can be considered as the basic function of this group. The other six functions can be uniquely defined through the floor function. can be considered as the basic function of this group. The other six functions can be uniquely defined through the floor function.
For real 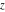 , the floor function , the floor function  is the greatest integer less than or equal to is the greatest integer less than or equal to 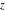 . .
For arbitrary complex  , the function , the function 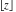 can be described (or defined) by the following formulas: can be described (or defined) by the following formulas:
Examples:  , , 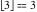 , ,  , ,  , , 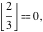 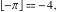 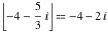 , , 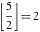 , , . .
For real 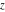 , the rounding function , the rounding function 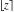 is the integer closest to is the integer closest to 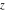 (if (if 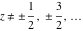 ). ).
For arbitrary 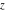 , the round function , the round function 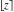 can be described (or defined) by the following formulas: can be described (or defined) by the following formulas:
Examples: 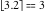 , , 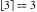 , ,  , , 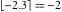 , , 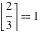 , , 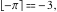 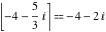 , ,  , , 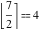 . .
For real 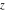 , the ceiling function , the ceiling function 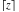 is the smallest integer greater than or equal to is the smallest integer greater than or equal to 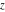 . .
For arbitrary  , the function , the function 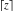 can be described (or defined) by the following formulas: can be described (or defined) by the following formulas:
Examples: 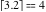 , , 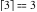 , , 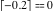 , , 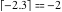 , , 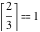 , , 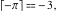 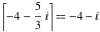 , , 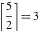 , ,  . .
For real 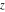 , the function integer part , the function integer part 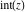 is the integer part of is the integer part of 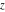 . .
For arbitrary  , the function , the function 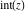 can be described (or defined) by the following formulas: can be described (or defined) by the following formulas:
Examples:  , , 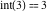 , , 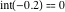 , , 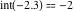 , ,  , , 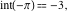 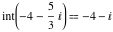 , , 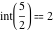 , , . .
For real 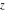 , the function fractional part , the function fractional part 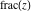 is the fractional part of is the fractional part of  . .
For arbitrary 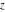 , the function , the function  can be described (or defined) by the following formulas: can be described (or defined) by the following formulas:
Examples: 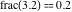 , , 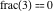 , , 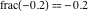 , , 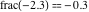 , , 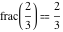 , , 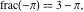 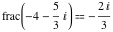 , , 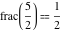 , ,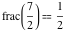 . .
For complex  and and  , the mod function , the mod function 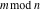 is the remainder of the division of is the remainder of the division of 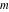 by by 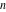 . The sign of . The sign of 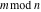 for real for real 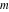 , , 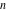 is always the same as the sign of is always the same as the sign of 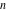 . .
The mod function 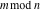 can be described (or defined) by the following formula: can be described (or defined) by the following formula:
The functional property  makes the behavior of makes the behavior of 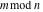 similar to the behavior of similar to the behavior of  . .
Examples: 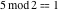 , , 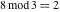 , , 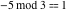 , ,  , , 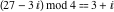 , , 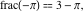 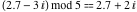 . .
For complex 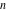 and and 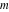 , the integer part of the quotient (quotient) function , the integer part of the quotient (quotient) function  is the integer quotient of is the integer quotient of 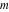 and and 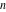 . .
The quotient function 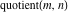 can be described (or defined) by the following formula: can be described (or defined) by the following formula:
Examples: 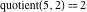 , , 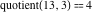 , , 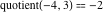 , , 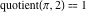 , ,  , , 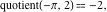 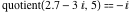 . .
|