|
The best-known properties and formulas of the GCD and LCM
Specific values for specialized variables
The functions GCD and LCM 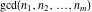 , , 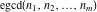 , and , and 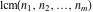 have the following values for specialized values: have the following values for specialized values:
The first values of the greatest common divisor (gcd(m, n)) of the integers 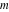 and and 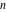 for for 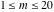 and and 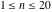 are described in the following table: are described in the following table:
The first values of the extended greatest common divisor (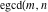 ) of the integers ) of the integers 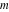 and and 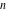 for for 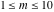 and and 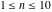 are described in the following table: are described in the following table:
The first values of the least common multiple (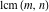 ) of the integers ) of the integers 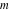 and and 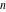 for for 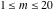 and and 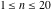 are described in the following table: are described in the following table:
Analyticity
The functions 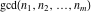 and and 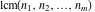 are nonanalytical functions defined over are nonanalytical functions defined over 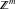 with values in with values in 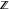 .
The function .
The function 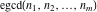 is a vector‐valued nonanalytical function defined over is a vector‐valued nonanalytical function defined over 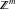 . .
Periodicity
All three functions 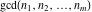 , , 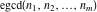 , and , and 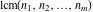 do not have periodicity. do not have periodicity.
Parity and symmetry
The functions 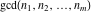 and and 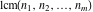 are even functions: are even functions:
The functions 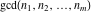 and and 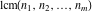 have permutation symmetry: have permutation symmetry:
Series representations
The function 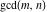 has the following sum representations: has the following sum representations:
where 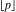 is the floor function and is the floor function and 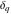 is the Kronecker delta function. is the Kronecker delta function.
Product representations
The functions 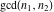 and and 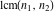 have the following product representations: have the following product representations:
Generating functions
The function 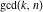 can be represented as the coefficients of the series expansion of corresponding generating functions, which includes a sum of the Euler totient function: can be represented as the coefficients of the series expansion of corresponding generating functions, which includes a sum of the Euler totient function:
Transformations with multiple arguments
The GCD and LCM functions 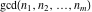 , , 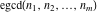 , and , and 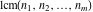 satisfy special relations including multiple arguments, for example: satisfy special relations including multiple arguments, for example:
Identities
The GCD and LCM functions satisfy some parallel identities that can be presented in the forms shown in the following table:
Summation
There are many finite and infinite sums containing GCD and LCM functions, for example:
Limit operation
The following two related limits include the function 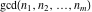 . The third limit includes lcm( . The third limit includes lcm(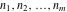 ): ):
Inequalities
The functions 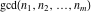 and and 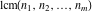 satisfy various inequalities, for example: satisfy various inequalities, for example:
|