|
Definitions of complex components
The complex components include six basic characteristics describing complex numbers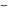 absolute value (modulus) absolute value (modulus) 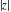 , argument (phase) , argument (phase) 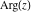 , real part , real part 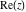 , imaginary part , imaginary part 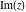 , complex conjugate , complex conjugate 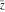 , and sign function (signum) , and sign function (signum) 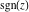 . It is impossible to define real and imaginary parts of the complex number . It is impossible to define real and imaginary parts of the complex number 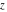 through other functions or complex characteristics. They are too basic, so their symbols can be described by simple sentences, for example, " through other functions or complex characteristics. They are too basic, so their symbols can be described by simple sentences, for example, "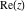 gives the real part of the number gives the real part of the number 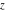 ," and " ," and "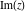 gives the imaginary part of the number gives the imaginary part of the number 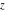 ." ."
All other complex components are defined by the following formulas:
Geometrically, the absolute value (or modulus) of a complex number 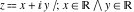 is the Euclidean distance from is the Euclidean distance from 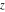 to the origin, which can also be described by the formula: to the origin, which can also be described by the formula:
Geometrically, the argument of a complex number 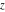 is the phase angle (in radians) that the line from 0 to is the phase angle (in radians) that the line from 0 to 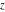 makes with the positive real axis. So, the complex number makes with the positive real axis. So, the complex number 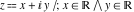 can be presented by the formulas: can be presented by the formulas:
Geometrically, the real part of a complex number 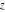 is the projection of the complex point is the projection of the complex point 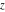 on the real axis. So, the real part of the complex number on the real axis. So, the real part of the complex number 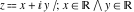 can be presented by the formulas: can be presented by the formulas:
Geometrically, the imaginary part of a complex number 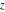 is the projection of complex point is the projection of complex point 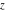 on the imaginary axis. So, the imaginary part of the complex number on the imaginary axis. So, the imaginary part of the complex number 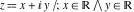 can be presented by the formulas: can be presented by the formulas:
Geometrically, the complex conjugate of a complex number 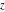 is the complex point is the complex point 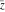 , which is symmetrical to , which is symmetrical to 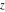 with respect to the real axis. So, the conjugate value with respect to the real axis. So, the conjugate value 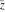 of the complex number of the complex number 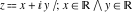 can be presented by the formulas: can be presented by the formulas:
Geometrically, the sign function (signum) is the complex point 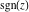 that lays on the intersection of the unit circle that lays on the intersection of the unit circle 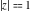 and the line from 0 to and the line from 0 to 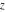 (if (if 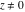 ). So, the conjugate value ). So, the conjugate value 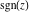 of the complex number of the complex number 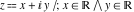 can be presented by the formulas: can be presented by the formulas:
|