|
There are four symbols discussed here—an indeterminate numerical quantity 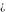 , infinity , infinity 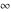 , complex infinity , complex infinity 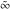 , and directed infinity in the complex plane , and directed infinity in the complex plane 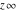 . They are defined as follows: . They are defined as follows:
Indeterminate 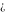 is a symbol that represents a numerical quantity whose magnitude cannot be determined. In particular, arbitrary functions with any argument being is a symbol that represents a numerical quantity whose magnitude cannot be determined. In particular, arbitrary functions with any argument being 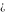 also becomes also becomes 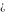 : : 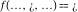 . .
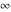 is a symbol that represents a positive infinite quantity. is a symbol that represents a positive infinite quantity.
∞~ represents an infinite numerical quantity whose direction in the complex plane is unknown (undetermined).
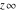 represents an infinite numerical quantity that is a positive real multiple of the complex number represents an infinite numerical quantity that is a positive real multiple of the complex number 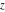 . .
|