|
Entering the complex plane   |
  |
Upper picture: 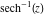 in the upper half of the in the upper half of the  near the real axis viewed from the lower half‐plane.
Lower picture: near the real axis viewed from the lower half‐plane.
Lower picture: 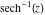 in the lower half of the in the lower half of the  near the real axis viewed from the upper half‐plane.
Here the complex variable near the real axis viewed from the upper half‐plane.
Here the complex variable 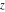 is expressed as is expressed as 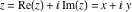 . The red surface is the real part of . The red surface is the real part of 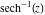 . The blue, semi‐transparent surface is the imaginary part of . The blue, semi‐transparent surface is the imaginary part of 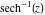 . The pink tube is the real part of the function . The pink tube is the real part of the function 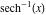 along the real axis and the skyblue tube is the imaginary part of the function along the real axis and the skyblue tube is the imaginary part of the function 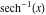 along the real axis. At along the real axis. At 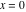 , the function , the function 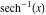 has a logarithmic singularity. The branch points at has a logarithmic singularity. The branch points at 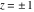 are of square root type. Along the real axis outside the interval are of square root type. Along the real axis outside the interval  , the real part of , the real part of  vanishes identically; going away from the real axis into the vanishes identically; going away from the real axis into the  gives a function that approaches 0. Along the real axis, the imaginary part of gives a function that approaches 0. Along the real axis, the imaginary part of 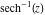 is piecewise constant inside the interval is piecewise constant inside the interval 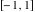 ; going away from the real axis into the ; going away from the real axis into the  is a function that approaches is a function that approaches 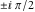 . The imaginary part is discontinuous along the branch cuts . The imaginary part is discontinuous along the branch cuts 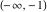 and and 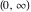 . The imaginary part has lower lip continuity in the . The imaginary part has lower lip continuity in the . . Branch cuts The real part and the imaginary part of  over the over the  . The left graphic shows . The left graphic shows 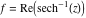 and the right graphic shows and the right graphic shows  . Along the intervals . Along the intervals 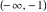 , , 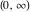 the function the function 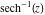 has branch cuts. The imaginary part has discontinuities along the branch cuts. At has branch cuts. The imaginary part has discontinuities along the branch cuts. At 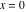 , the function , the function 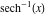 has a logarithmic branch point. The branch points at has a logarithmic branch point. The branch points at 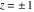 are of square root type. The viewpoint is from the upper half‐plane. are of square root type. The viewpoint is from the upper half‐plane. The real part and the imaginary part of 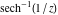 over the over the  . The left graphic shows . The left graphic shows 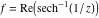 and the right graphic shows and the right graphic shows 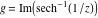 . Around . Around 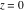 , the function , the function 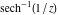 has disconnected sheets. The viewpoint is from the lower half‐plane. has disconnected sheets. The viewpoint is from the lower half‐plane. The branch cuts of the real part and the imaginary part of  over the over the  . The left graphic shows . The left graphic shows  and the right graphic shows and the right graphic shows  . The red and blue vertical surfaces connect points from the immediate lower and upper neighborhood of the branch cuts. The branch point at . The red and blue vertical surfaces connect points from the immediate lower and upper neighborhood of the branch cuts. The branch point at 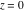 is a logarithmic branch point and branch points at is a logarithmic branch point and branch points at 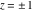 are of square root type. Only the imaginary part shows discontinuities due to the branch cuts. The viewpoint is from the upper half‐plane. At are of square root type. Only the imaginary part shows discontinuities due to the branch cuts. The viewpoint is from the upper half‐plane. At  two branch cuts start to coincide, but only one branch point is there. two branch cuts start to coincide, but only one branch point is there. The branch cuts of the real part and the imaginary part of 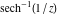 over the over the 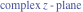 . The left graphic shows . The left graphic shows 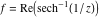 and the right graphic shows and the right graphic shows 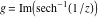 . The red and blue vertical surfaces connect points from the immediate lower and upper neighborhood of the branch cuts. Around . The red and blue vertical surfaces connect points from the immediate lower and upper neighborhood of the branch cuts. Around 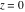 , the function , the function 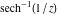 has disconnected sheets. Only the imaginary part shows discontinuities due to the branch cuts. The viewpoint is from the lower half‐plane. has disconnected sheets. Only the imaginary part shows discontinuities due to the branch cuts. The viewpoint is from the lower half‐plane. Real part over the complex plane The real part of 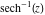 where where  . The surface is colored according to the imaginary part. The right graphic is a contour plot of the scaled real part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. The function . The surface is colored according to the imaginary part. The right graphic is a contour plot of the scaled real part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. The function 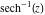 has a logarithmic singularity at has a logarithmic singularity at 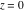 , and on the real axis its real part vanishes identically outside the interval , and on the real axis its real part vanishes identically outside the interval  ; going away from the real axis into the upper half of the ; going away from the real axis into the upper half of the  gives a function that asymptotically approaches 0. gives a function that asymptotically approaches 0.  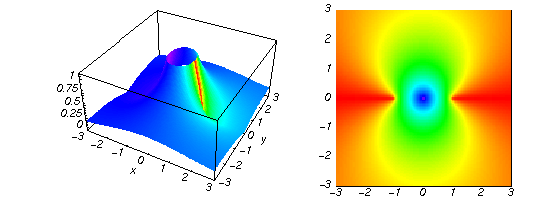 |
The absolute value of the real part of 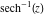 where where  . The surface is colored according to the absolute value of the imaginary part. The right graphic is a contour plot of the scaled absolute value of the real part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. The function . The surface is colored according to the absolute value of the imaginary part. The right graphic is a contour plot of the scaled absolute value of the real part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. The function 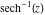 has a logarithmic singularity at has a logarithmic singularity at 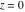 , and on the real axis its real part vanishes identically outside the interval , and on the real axis its real part vanishes identically outside the interval 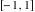 ; going away from the real axis into the upper half of the ; going away from the real axis into the upper half of the  gives a function that asymptotically approaches 0. gives a function that asymptotically approaches 0. Imaginary part over the complex plane The imaginary part of 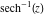 where where 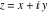 . The surface is colored according to the real part. The right graphic is a contour plot of the scaled imaginary part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. Along the real axis, the imaginary part of . The surface is colored according to the real part. The right graphic is a contour plot of the scaled imaginary part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. Along the real axis, the imaginary part of 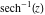 is piecewise constant inside the interval is piecewise constant inside the interval  ; going away from the real axis into the ; going away from the real axis into the  gives function that approaches gives function that approaches  . .  is a discontinuous function over the is a discontinuous function over the 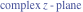 . The branch point at . The branch point at 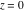 is a logarithmic branch point, and branch points at is a logarithmic branch point, and branch points at 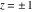 are of square root type. are of square root type.  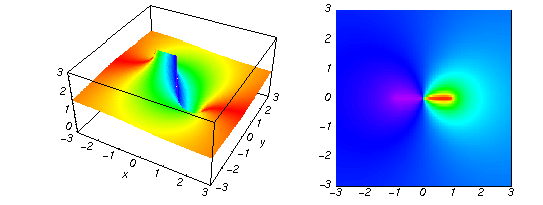 |
The absolute value of the imaginary part of  where where 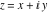 . The surface is colored according to the absolute value of the real part. The right graphic is a contour plot of the scaled absolute value of the imaginary part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. Along the real axis, the imaginary part of . The surface is colored according to the absolute value of the real part. The right graphic is a contour plot of the scaled absolute value of the imaginary part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. Along the real axis, the imaginary part of 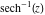 is piecewise constant inside the interval is piecewise constant inside the interval 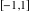 ; going away from the real axis into the ; going away from the real axis into the  gives function that approaches gives function that approaches 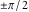 . .  is a discontinuous function over the is a discontinuous function over the  . The branch point at . The branch point at 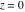 is a logarithmic branch point, and branch points at is a logarithmic branch point, and branch points at 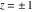 are of square root type. are of square root type. Absolute value part over the complex plane The absolute value of 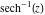 where where  . The surface is colored according to the argument. The right graphic is a contour plot of the scaled absolute value, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. . The surface is colored according to the argument. The right graphic is a contour plot of the scaled absolute value, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. Argument over the complex plane The argument of 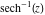 where where 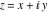 . The surface is colored according to the absolute value. The right graphic is a contour plot of the scaled argument, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. . The surface is colored according to the absolute value. The right graphic is a contour plot of the scaled argument, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest.  has lines of discontinuities over the has lines of discontinuities over the  . . The square of the sine of the argument of 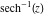 where where 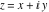 . For dominantly real values, the function values are near 0, and for dominantly imaginary values, the function values are near 1. The surface is colored according to the absolute value. The right graphic is a cyclically colored contour plot of the argument. Red represents arguments near . For dominantly real values, the function values are near 0, and for dominantly imaginary values, the function values are near 1. The surface is colored according to the absolute value. The right graphic is a cyclically colored contour plot of the argument. Red represents arguments near  and light‐blue represents arguments near 0. and light‐blue represents arguments near 0. Zero-pole plot The logarithm of the absolute value of 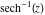 where where 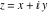 in the upper half‐plane. The surface is colored according to the square of the argument. In this plot, zeros are easily visible as spikes extending downwards and poles and logarithmic singularities as spikes extending upwards. The logarithmic branch point at in the upper half‐plane. The surface is colored according to the square of the argument. In this plot, zeros are easily visible as spikes extending downwards and poles and logarithmic singularities as spikes extending upwards. The logarithmic branch point at 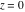 and the square root branch point at and the square root branch point at 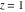 are visible. are visible. Real part over the complex plane near infinity The real part of 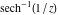 where where  . The surface is colored according to the imaginary part. The right graphic is a contour plot of the scaled real part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. At . The surface is colored according to the imaginary part. The right graphic is a contour plot of the scaled real part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. At  the function the function 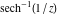 has no singularity. has no singularity. The absolute value of the real part of 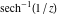 where where 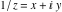 . The surface is colored according to the absolute value of the imaginary part. The right graphic is a contour plot of the scaled absolute value of the real part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. . The surface is colored according to the absolute value of the imaginary part. The right graphic is a contour plot of the scaled absolute value of the real part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. Imaginary part over the complex plane near infinity The imaginary part of 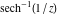 where where  . The surface is colored according to the real part. The right graphic is a contour plot of the scaled imaginary part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. . The surface is colored according to the real part. The right graphic is a contour plot of the scaled imaginary part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. The absolute value of the imaginary part of 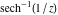 where where 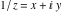 . The surface is colored according to the absolute value of the real part. The right graphic is a contour plot of the scaled absolute value of the imaginary part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. . The surface is colored according to the absolute value of the real part. The right graphic is a contour plot of the scaled absolute value of the imaginary part, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. Absolute value part over the complex plane near infinity The absolute value of 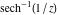 where where  . The surface is colored according to the argument. The right graphic is a contour plot of the scaled absolute value, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. . The surface is colored according to the argument. The right graphic is a contour plot of the scaled absolute value, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. Argument over the complex plane near infinity The argument of 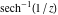 where where 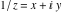 . The surface is colored according to the absolute value. The right graphic is a contour plot of the scaled argument, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. . The surface is colored according to the absolute value. The right graphic is a contour plot of the scaled argument, meaning the height values of the left graphic translate into color values in the right graphic. Red is smallest and violet is largest. The square of the sine of the argument of 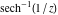 where where 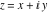 . For dominantly real values the functions values are near 0 and for dominantly imaginary values the function values are near 1. The surface is colored according to the absolute value. The right graphic is a cyclically colored contour plot of the argument. Red represents arguments near . For dominantly real values the functions values are near 0 and for dominantly imaginary values the function values are near 1. The surface is colored according to the absolute value. The right graphic is a cyclically colored contour plot of the argument. Red represents arguments near 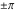 and light‐blue represents arguments near 0. and light‐blue represents arguments near 0. Zero-pole plot near infinity The logarithm of the absolute value of 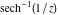 where where 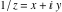 in the upper half‐plane. The surface is colored according to the square of the argument. In this plot zeros are easily visible as spikes extending downwards and poles and logarithmic singularities as spikes extending upwards. in the upper half‐plane. The surface is colored according to the square of the argument. In this plot zeros are easily visible as spikes extending downwards and poles and logarithmic singularities as spikes extending upwards.
|