|
Recurrence plots Recurrence plot of 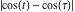 over the over the 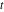 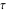 ‐plane. ‐plane. Bifurcation-related plots Nestings of the map 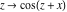 starting with starting with 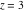 as a function of as a function of 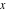 . The number of iterations increases from red (0) to blue (80). . The number of iterations increases from red (0) to blue (80). Nestings of the map 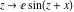 starting with starting with 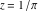 as a function of as a function of 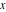 . The initial iterations are ignored. . The initial iterations are ignored. Iterations and powers in the complex plane The real part and the imaginary part of the scaled value of 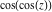 in the in the 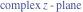 . The left graphic shows the real part and the right graphic shows the imaginary part. . The left graphic shows the real part and the right graphic shows the imaginary part. The real part and the imaginary part of the scaled value of 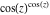 in the in the 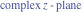 . The left graphic shows the real part and the right graphic shows the imaginary part. . The left graphic shows the real part and the right graphic shows the imaginary part. Lattice sums The real part and the imaginary part of the lattice sum 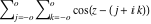 in the in the 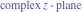 . The left graphic shows the real part and the right graphic shows the imaginary part. Because . The left graphic shows the real part and the right graphic shows the imaginary part. Because 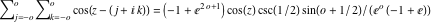 , one basically recovers the function , one basically recovers the function 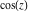 (modulo a (modulo a  ‐independent factor). ‐independent factor). Fractals and Julia sets Mandelbrot set of the map 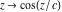 over the over the 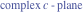 . The coloring indicates the number of iterations before . The coloring indicates the number of iterations before 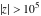 . . Julia sets of the map 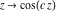 over the over the  . .
|