|
Over the Re(a)Re(z)-plane The real part, the imaginary part, the absolute value, and the argument of the function 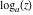 over the over the 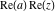 ‐plane. ‐plane. The real part, the imaginary part, the absolute value, and the argument of the function 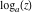 over the over the 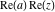 ‐plane around ‐plane around 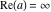 . . The real part, the imaginary part, the absolute value, and the argument of the function 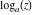 over the over the 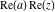 ‐plane around ‐plane around 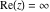 . . The real part, the imaginary part, the absolute value, and the argument of the function 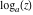 over the over the 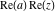 ‐plane around ‐plane around 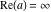 and and 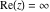 . . Over the Re(a)Im(z)-plane The real part, the imaginary part, the absolute value, and the argument of the function 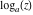 over the over the 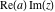 ‐plane. ‐plane. The real part, the imaginary part, the absolute value, and the argument of the function 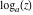 over the over the 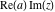 ‐plane around ‐plane around 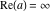 . . The real part, the imaginary part, the absolute value, and the argument of the function 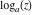 over the over the 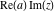 ‐plane around ‐plane around 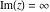 . . The real part, the imaginary part, the absolute value, and the argument of the function 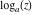 over the over the 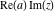 ‐plane around ‐plane around 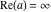 and and 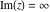 . . Over the Im(a)Re(z)-plane The real part, the imaginary part, the absolute value, and the argument of the function 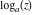 over the over the 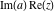 ‐plane. ‐plane. The real part, the imaginary part, the absolute value, and the argument of the function 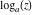 over the over the 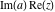 ‐plane around ‐plane around 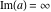 . . The real part, the imaginary part, the absolute value, and the argument of the function 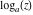 over the over the 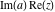 ‐plane around ‐plane around 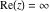 . . The real part, the imaginary part, the absolute value, and the argument of the function 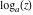 over the over the 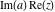 ‐plane around ‐plane around 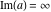 and and 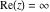 . . Over the Im(a)Im(z)-plane The real part, the imaginary part, the absolute value, and the argument of the function 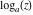 over the over the 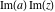 ‐plane. ‐plane. The real part, the imaginary part, the absolute value, and the argument of the function 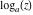 over the over the 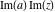 ‐plane around ‐plane around 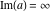 . . The real part, the imaginary part, the absolute value, and the argument of the function 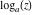 over the over the 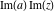 ‐plane around ‐plane around 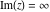 . . The real part, the imaginary part, the absolute value, and the argument of the function 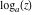 over the over the 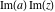 ‐plane around ‐plane around 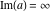 and and 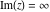 . . Over the unit circle planes The real part, the imaginary part, the absolute value, and the argument of the function 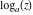 over the over the 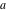 ‐unit circle, ‐unit circle, 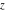 ‐unit circle‐plane. ‐unit circle‐plane.
|