|
The elliptic logarithm 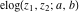 is the particular case of the hypergeometric function of two variables (Appell function is the particular case of the hypergeometric function of two variables (Appell function 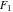 ): ):
The elliptic exponent 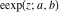 is connected with Jacobi amplitude by the following formula: is connected with Jacobi amplitude by the following formula:
The elliptic exponent 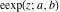 and elliptic logarithm and elliptic logarithm  can be expressed through direct and inverse Weierstrass functions by the following formulas: can be expressed through direct and inverse Weierstrass functions by the following formulas:
The elliptic logarithm 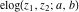 has the following representation through incomplete elliptic integral has the following representation through incomplete elliptic integral 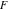 : :
The elliptic logarithm 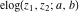 is the inverse function to the elliptic exponent is the inverse function to the elliptic exponent 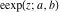 and its derivative and its derivative 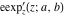 . Relations between them are described by the following formulas: . Relations between them are described by the following formulas:
|