|
The best-known properties and formulas for elliptic exp and elliptic log
Values at zero
The elliptic exponent 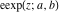 , its derivative , its derivative 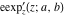 , and the elliptic logarithm , and the elliptic logarithm 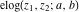 have the following values at the origin point: have the following values at the origin point:
Specific values for specialized parameter
The elliptic exponent 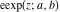 has the following value at the specialized point has the following value at the specialized point 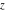 : :
Analyticity
The elliptic exponent 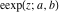 and its derivative and its derivative 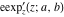 are vector‐valued functions of are vector‐valued functions of 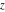 , , 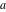 , and , and 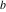 , which are analytic in each component, and they are defined over , which are analytic in each component, and they are defined over 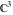 . .
The elliptic logarithm 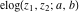 is an analytical function of is an analytical function of 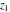 , , 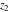 , , 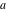 , , 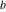 , which is defined in , which is defined in 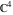 . .
The elliptic exponent 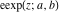 , its derivative , its derivative 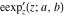 , and the elliptic logarithm , and the elliptic logarithm 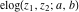 have complicated branch cuts. have complicated branch cuts.
Poles and essential singularities
The elliptic logarithm 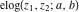 does not have poles and essential singularities. does not have poles and essential singularities.
Periodicity
The elliptic exponent 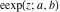 , its derivative , its derivative 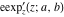 , and the elliptic logarithm , and the elliptic logarithm 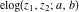 do not have periodicity. do not have periodicity.
Parity and symmetry
The elliptic exponent 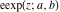 , its derivative , its derivative 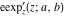 , and the elliptic logarithm , and the elliptic logarithm 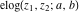 have mirror symmetry: have mirror symmetry:
Integral representations
The elliptic logarithm 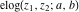 has the following integral representation: has the following integral representation:
Identities
The elliptic exponent 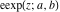 satisfies the following identities including the complete elliptic integral satisfies the following identities including the complete elliptic integral 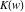 : :
Simple representations of derivatives
The first derivatives of elliptic exponent 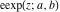 and the elliptic logarithm and the elliptic logarithm 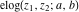 have the following representations: have the following representations:
Differential equations
The elliptic exponent 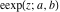 , its derivative , its derivative 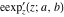 , and the elliptic logarithm , and the elliptic logarithm 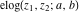 satisfy the following ordinary nonlinear differential equations: satisfy the following ordinary nonlinear differential equations:
|