|
Introduction to the inverse Jacobi elliptic functions
General
Definitions of the inverse Jacobi functions
The inverses of the twelve Jacobi elliptic functions 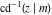 , , 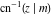 , , 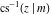 , , 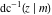 , , 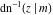 , , 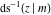 , , 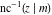 , , 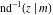 , , 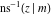 , , 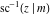 , , 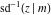 , and , and 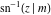 are defined by the following formulas: are defined by the following formulas:
It is obvious that the inverses of the twelve Jacobi elliptic functions are actually the definite elliptic integrals and can be expressed through the Legendre elliptic integrals.
A quick look at the inverse Jacobi functions Here is a quick look at the graphics for the inverse Jacobi functions along the real axis.
Connections within the group of inverse Jacobi functions and with other related function groups Representations through more general functions Representations through related equivalent functions Relations to inverse functions Representations through other inverse Jacobi functions Representations of 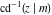 through other inverse Jacobi functions are: through other inverse Jacobi functions are: Representations of 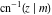 through other inverse Jacobi functions are: through other inverse Jacobi functions are: Representations of 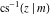 through other inverse Jacobi functions are: through other inverse Jacobi functions are: Representations of 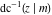 through other inverse Jacobi functions are: through other inverse Jacobi functions are: Representations of 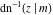 through other inverse Jacobi functions are: through other inverse Jacobi functions are: Representations of 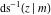 through other inverse Jacobi functions are: through other inverse Jacobi functions are: Representations of 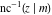 through other inverse Jacobi functions are: through other inverse Jacobi functions are: Representations of 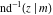 through other inverse Jacobi functions are: through other inverse Jacobi functions are: Representations of 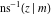 through other inverse Jacobi functions are: through other inverse Jacobi functions are: Representations of 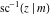 through other inverse Jacobi functions are: through other inverse Jacobi functions are: Representations of 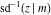 through other inverse Jacobi functions are: through other inverse Jacobi functions are: Representations of 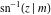 through other inverse Jacobi functions are: through other inverse Jacobi functions are:
The best-known properties and formulas for inverse Jacobi functions
Simple values at zero
The inverse Jacobi functions 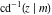 , , 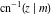 , , 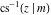 , , 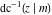 , , 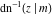 , , 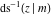 , , 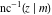 , , 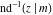 , , 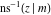 , , 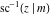 , , 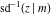 , and , and 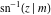 have the following simple values at the origin: have the following simple values at the origin:
Specific values for specialized parameter values
The inverse Jacobi functions 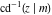 , , 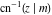 , , 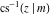 , , 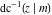 , , 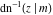 , , 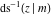 , , 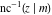 , , 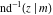 , , 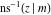 , , 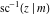 , , 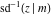 , and , and 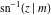 can be represented through elementary functions when can be represented through elementary functions when 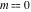 or or 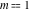 . In these cases they degenerate into inverse trigonometric and inverse hyperbolic functions. If . In these cases they degenerate into inverse trigonometric and inverse hyperbolic functions. If 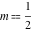 , they can be represented through the elliptic integrals , they can be represented through the elliptic integrals 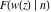 and and  : :
At the points 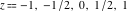 , and , and 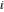 , the inverse Jacobi functions , the inverse Jacobi functions 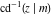 , , 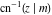 , , 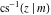 , , 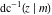 , , 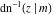 , , 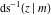 , , 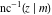 , , 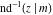 , , 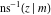 , , 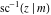 , , 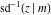 , , 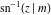 have the following representations through the elliptic integrals have the following representations through the elliptic integrals 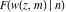 and and  : :
At the points 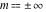 or or 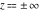 , the inverse Jacobi functions , the inverse Jacobi functions  , , 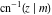 , , 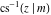 , , 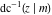 , , 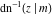 , , 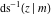 , , 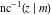 , , 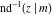 , , 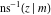 , , 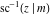 , , 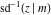 , and , and 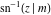 have the following values: have the following values:
Analyticity
The inverse Jacobi functions 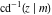 , , 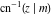 , , 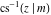 , , 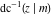 , , 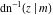 , , 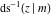 , , 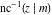 , , 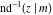 , , 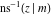 , , 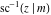 , , 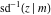 , and , and 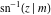 are analytical functions of are analytical functions of 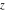 and and 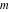 that are defined over that are defined over 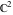 . .
Poles and essential singularities
The inverse Jacobi functions 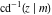 , , 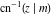 , , 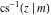 , , 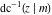 , , 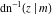 , , 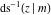 , , 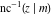 , , 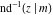 , , 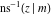 , , 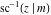 , , 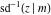 , and , and 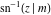 do not have poles and essential singularities with respect to do not have poles and essential singularities with respect to 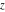 and and 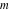 . .
Branch points and branch cuts
For fixed 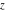 , the point , the point 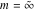 is the branch point for all twelve inverse Jacobi functions. Other branch points are the following: is the branch point for all twelve inverse Jacobi functions. Other branch points are the following: 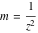 for for 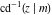 , , 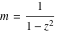 for for 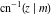 , , 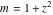 for for 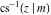 , , 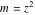 for for 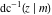 , , 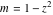 for for 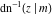 , , 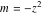 and and 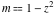 for for 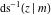 , , 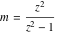 for for 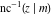 , , 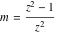 for for 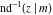 , , 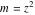 for for 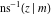 , , 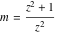 for for 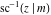 , , 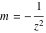 and and 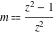 for for 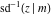 , and , and 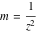 for for 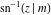 . .
For fixed 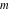 , the point , the point 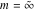 is the branch point for all twelve inverse Jacobi functions. There are four or five other branch points that include the following: is the branch point for all twelve inverse Jacobi functions. There are four or five other branch points that include the following: 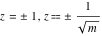 for for 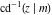 , , 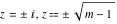 for for 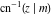 , , 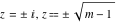 for for 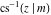 , , 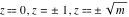 for for 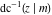 , , 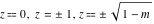 for for 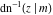 , , 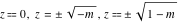 for for 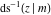 , , 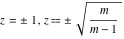 for for 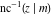 , , 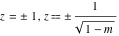 for for 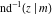 , , 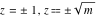 for for 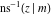 , , 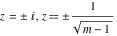 for for 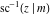 , , 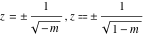 for for 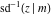 , and , and 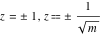 for for 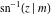 . .
Parity and symmetry
The inverse Jacobi functions 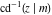 , , 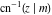 , , 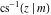 , , 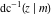 , , 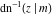 , , 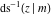 , , 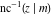 , , 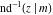 , , 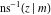 , , 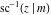 , , 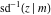 , and , and 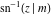 have mirror symmetry: have mirror symmetry:
Nine inverse Jacobi functions 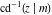 , , 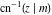 , , 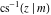 , , 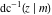 , , 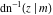 , , 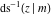 , , 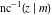 , , 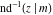 , , 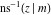 have the following quasi‐reflection symmetry with respect to have the following quasi‐reflection symmetry with respect to 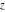 : :
The other three inverse Jacobi functions 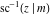 , , 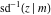 , and , and 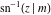 are odd functions with respect to are odd functions with respect to 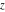 : :
Series representations
The inverse Jacobi functions 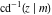 , , 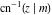 , , 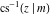 , , 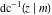 , , 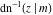 , , 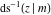 , , 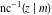 , , 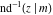 , , 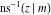 , , 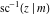 , , 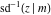 , and , and 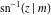 have the following series expansions at the point have the following series expansions at the point 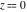 : :
The previous expansions are the particular cases of the following series representations of the twelve inverse Jacobi functions near the point 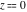 : :
The inverse Jacobi functions 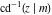 , , 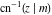 , , 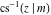 , , 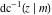 , , 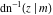 , , 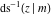 , , 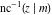 , , 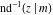 , , 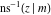 , , 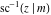 , , 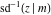 , and , and 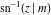 have the following series expansions at the point have the following series expansions at the point 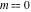 : :
The previous expansions are the particular cases of the following series representations of the twelve inverse Jacobi functions near the point 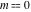 : :
Integral representations
The inverse Jacobi functions 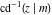 , , 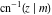 , , 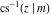 , , 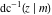 , , 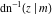 , , 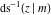 , , 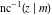 , , 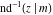 , , 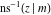 , , 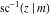 , , 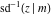 , and , and 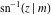 have the following integral representations, which can be used for their definitions: have the following integral representations, which can be used for their definitions:
Transformations
Some inverse Jacobi functions satisfy additional formulas, for example:
Identities
The inverse Jacobi functions 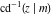 , , 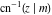 , , 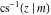 , , 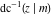 , , 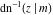 , , 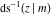 , , 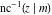 , , 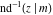 , , 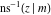 , , 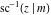 , , 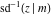 , and , and 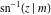 satisfy nonlinear functional equations: satisfy nonlinear functional equations:
Representations of derivatives
The derivatives of the inverse Jacobi functions 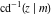 , , 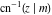 , , 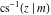 , , 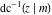 , ,  , , 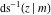 , , 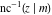 , , 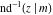 , , 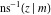 , , 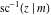 , , 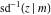 , and , and 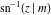 with respect to variable with respect to variable 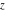 can be expressed through direct and inverse Jacobi functions: can be expressed through direct and inverse Jacobi functions:
The previous formulas can be generalized to the following symbolic derivatives of the 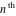 order with respect to variable order with respect to variable 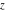 : :
The derivatives of the inverse Jacobi functions 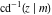 , , 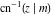 , , 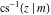 , , 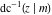 , , 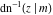 , , 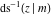 , , 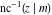 , , 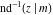 , , 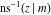 , , 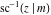 , , 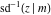 , and , and 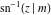 with respect to variable with respect to variable 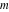 have more complicated representations that include direct and inverse Jacobi functions and the elliptic integral have more complicated representations that include direct and inverse Jacobi functions and the elliptic integral 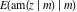 : :
The previous formulas can be generalized to the following symbolic derivatives of the 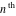 order with respect to variable order with respect to variable 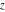 : :
Integration
The indefinite integrals of the twelve inverse Jacobi functions 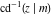 , , 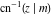 , , 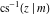 , , 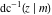 , , 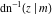 , , 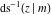 , , 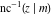 , , 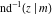 , , 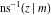 , , 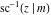 , , 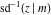 , and , and 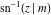 with respect to variable with respect to variable 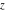 can be expressed through direct and inverse Jacobi and elementary functions by the following formulas: can be expressed through direct and inverse Jacobi and elementary functions by the following formulas:
The indefinite integrals of the twelve inverse Jacobi functions 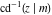 , , 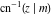 , , 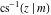 , , 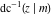 , , 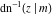 , , 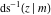 , , 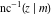 , , 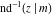 , , 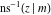 , , 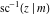 , , 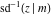 , and , and 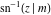 with respect to variable with respect to variable 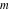 can be expressed through direct and inverse Jacobi and elementary functions by the following formulas: can be expressed through direct and inverse Jacobi and elementary functions by the following formulas:
Differential equations
The twelve inverse Jacobi functions 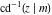 , , 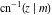 , , 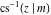 , , 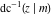 , , 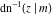 , , 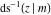 , , 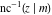 , , 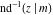 , , 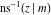 , , 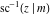 , , 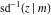 , and , and 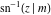 are the special solutions of the following second-order ordinary nonlinear differential equations: are the special solutions of the following second-order ordinary nonlinear differential equations:
Applications of the inverse Jacobi functions
Fields of application of the inverse Jacobi functions include most of the application areas of the direct functions. In many applications, the need for the inversion of the elliptic function fortunately does not arise. In cases where inversion is needed, the invese Jacobi elliptic functions are very useful tools for calculations.
|