|
Connections within the group of Weierstrass functions and inverses and with other function groups
Representations through more general functions
The Weierstrass elliptic 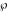 function function  and its inverse and its inverse 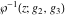 can be represented through the more general hypergeometric Appell can be represented through the more general hypergeometric Appell 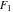 function of two variables by the following formulas: function of two variables by the following formulas:
Representations through related equivalent functions
The Weierstrass functions 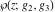 , , 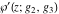 , , 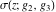 , ,  , ,  , , 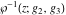 , and , and 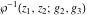 can be represented through some related equivalent functions, for example, through Jacobi functions: can be represented through some related equivalent functions, for example, through Jacobi functions:
where 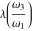 is modular lambda function, or through theta functions: is modular lambda function, or through theta functions:
or through elliptic integrals and the inverse elliptic nome:
Relations to inverse functions
The Weierstrass function 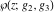 and its derivative and its derivative 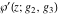 are interconnected with the inverse functions are interconnected with the inverse functions 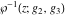 and and 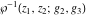 by the following formulas: by the following formulas:
Representations through other Weierstrass functions
Each of the Weierstrass functions 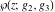 , , 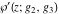 , ,  , , 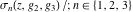 , and , and 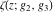 can be expressed through the other Weierstrass functions using numerous formulas, for example: can be expressed through the other Weierstrass functions using numerous formulas, for example:
Note that the Weierstrass functions 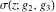 , , 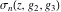 , , 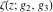 , , 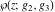 , and , and 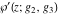 form a chain with respect to differentiation: form a chain with respect to differentiation:
|