|
Elliptic integrals were introduced in the investigations of J. Wallis (1655–1659) who studied the integral (in modern notation):
L. Euler (1733, 1757, 1763, 1766) derived the addition theorem for the following elliptic integrals currently called incomplete elliptic integrals of the first and second kind:
J.‐L. Lagrange (1783) and especially A. M. Legendre (1793, 1811, 1825–1828) devoted considerable attention to study different properties of these integrals. C. F. Gauss (1799, 1818) also used these integrals during his research.
Simultaneously, A. M. Legendre (1811) introduced the incomplete elliptic integral of the third kind:
and the complete versions of the integrals:
C. G. J. Jacobi (1827–1829) introduced inverse functons of the elliptic integrals 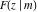 and and 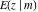 , which lead him to build the theory of elliptic functions. In 1829 C. G. J. Jacobi defined the function: , which lead him to build the theory of elliptic functions. In 1829 C. G. J. Jacobi defined the function:
which was later called the Jacobi zeta function. J. Liouville (1840) also studied the elliptic integrals 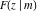 and and 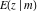 . .
N. H. Abel independently derived some of C. G. J. Jacobi's results and studied the so-called hyperelliptic and Abelian integrals.
|