|
The factorial 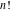 , double factorial , double factorial 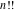 , Pochhammer symbol , Pochhammer symbol  , binomial coefficient , binomial coefficient 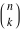 , and multinomial coefficient , and multinomial coefficient 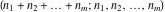 are defined by the following formulas. The first formula is a general definition for the complex arguments, and the second one is for positive integer arguments: are defined by the following formulas. The first formula is a general definition for the complex arguments, and the second one is for positive integer arguments:
Remark about values at special points: For 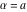 and and 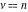 integers with integers with 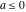 and and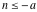 , the Pochhammer symbol , the Pochhammer symbol 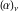 cannot be uniquely defined by a limiting procedure based on the previous definition because the two variables cannot be uniquely defined by a limiting procedure based on the previous definition because the two variables  and and 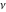 can approach the integers can approach the integers 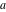 and and 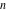 with with 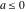 and and 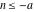 at different speeds. For such integers with at different speeds. For such integers with 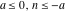 , the following definition is used: , the following definition is used:
Similarly, for 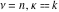 negative integers with negative integers with 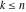 , the binomial coefficient , the binomial coefficient  cannot be uniquely defined by a limiting procedure based on the previous definition because the two variables cannot be uniquely defined by a limiting procedure based on the previous definition because the two variables 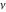 , , 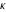 can approach negative integers can approach negative integers 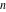 , , 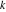 with with 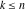 at different speeds. For negative integers with at different speeds. For negative integers with  , the following definition is used: , the following definition is used:
The previous symbols are interconnected and belong to one group that can be called factorials and binomials. These symbols are widely used in the coefficients of series expansions for the majority of mathematical functions.
|