|
The best-known properties and formulas for factorials and binomials
Real values for real arguments
For real values of arguments, the values of the factorials and binomials 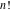 , , 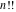 , , 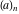 , , 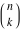 , and , and 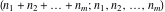 are real (or infinity). are real (or infinity).
Simple values at zero
The factorials and binomials 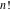 , , 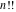 , , 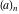 , , 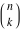 , and , and 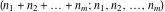 have simple values for zero arguments: have simple values for zero arguments:
Values at fixed points
Students usually learn the following basic table of values of the factorials 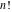 and and 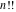 in special integer points: in special integer points:
Specific values for specialized variables
If variable 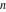 is a rational or integer number, the factorials is a rational or integer number, the factorials 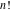 and and 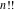 can be represented by the following general formulas: can be represented by the following general formulas:
For some particular values of the variables, the Pochhammer symbol 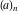 has the following meanings: has the following meanings:
Some well‐known formulas for binomial and multinomial functions are:
Analyticity
The factorials and binomials 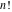 , , 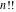 , , 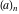 , , 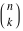 , and , and 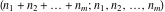 are defined for all complex values of their variables. The factorials, binomials, and multinomials are analytical functions of their variables and do not have branch cuts and branch points. The functions are defined for all complex values of their variables. The factorials, binomials, and multinomials are analytical functions of their variables and do not have branch cuts and branch points. The functions 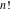 and and 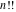 do not have zeros: do not have zeros: 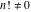 ; ; 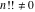 . Therefore, the functions . Therefore, the functions 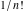 and and 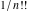 are entire functions with an essential singular point at are entire functions with an essential singular point at 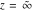 . .
Poles and essential singularities
The factorials and binomials 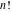 , , 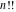 , , 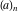 , , 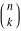 , and , and 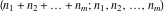 have an essential singularity for infinite values of any argument. This singular point is also the point of convergence of the poles (except have an essential singularity for infinite values of any argument. This singular point is also the point of convergence of the poles (except 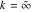 for for 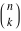 ). ).
The function 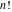 has an infinite set of singular points: has an infinite set of singular points: 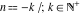 are the simple poles with residues are the simple poles with residues 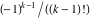 . .
The function 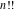 has an infinite set of singular points: has an infinite set of singular points: 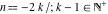 are the simple poles with residues are the simple poles with residues 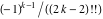 . .
For fixed 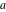 , the function , the function 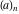 has an infinite set of singular points: has an infinite set of singular points: 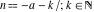 are the simple poles with residues are the simple poles with residues 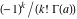 . .
For fixed 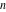 , the function , the function 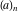 has an infinite set of singular points: has an infinite set of singular points: 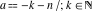 are the simple poles with residues are the simple poles with residues 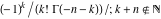 . .
For fixed 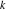 , the function , the function 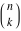 has an infinite set of singular points: has an infinite set of singular points: 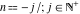 are the simple poles with residues are the simple poles with residues 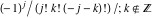 . .
By variable 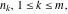 (with the other variables fixed) the function (with the other variables fixed) the function 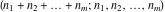 has an infinite set of singular points: has an infinite set of singular points: 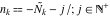 are the simple poles with residues are the simple poles with residues
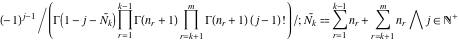 . .
Periodicity
The factorials and binomials 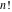 , , 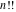 , , 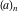 , , 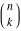 , and , and 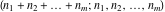 do not have periodicity. do not have periodicity.
Parity and symmetry
The factorials and binomials 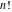 , , 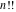 , , 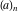 , , 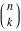 , and , and 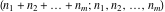 have mirror symmetry: have mirror symmetry:
The multinomial 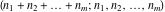 has permutation symmetry: has permutation symmetry:
Series representations
The factorials 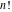 , , 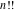 , and , and 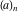 have the following series expansions in the regular points: have the following series expansions in the regular points:
The series expansions of 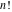 and and 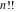 near singular points are given by the following formulas: near singular points are given by the following formulas:
Asymptotic series expansions
The asymptotic behavior of the factorials and binomials 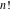 , , 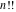 , , 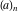 , , 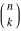 , , 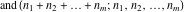 can be described by the following formulas (only the main terms of asymptotic expansion are given). The first is the famous Stirling's formula: can be described by the following formulas (only the main terms of asymptotic expansion are given). The first is the famous Stirling's formula:
Integral representations
The factorial 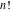 and binomial and binomial  can also be represented through the following integrals: can also be represented through the following integrals:
Transformations
The following formulas describe some of the main types of transformations between and among factorials and binomials:
Some of these transformations can be called addition formulas, for example:
Multiple argument transformations are, for example:
The following transformations are for products of the functions:
Identities
The factorials 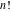 and and 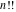 can be defined as the solutions of the following corresponding functional equations: can be defined as the solutions of the following corresponding functional equations:
The factorial 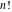 is the unique nonzero solution of the functional equation is the unique nonzero solution of the functional equation 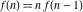 that is logarithmically convex for all real that is logarithmically convex for all real 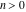 ; that is, for which ; that is, for which 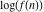 is a convex function for is a convex function for 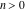 . .
The factorials and binomials 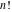 , , 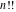 , , 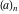 , , 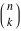 , and , and 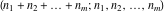 satisfy the following recurrence identities: satisfy the following recurrence identities:
The previous formulas can be generalized to the following recurrence identities with a jump of length n:
The Pochhammer symbol 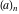 and binomial and binomial 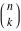 satisfy the following functional identities: satisfy the following functional identities:
Representations of derivatives
The derivatives of the functions 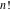 , , 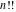 , , 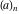 , , 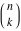 , , 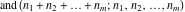 have rather simple representations that include the corresponding functions as factors: have rather simple representations that include the corresponding functions as factors:
The symbolic derivatives of the 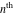 order form factorials and binomials order form factorials and binomials 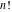 , , 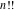 , , 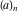 , , 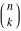 , and , and 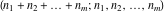 have much more complicated representations, which can include recursive function calls, regularized generalized hypergeometric functions have much more complicated representations, which can include recursive function calls, regularized generalized hypergeometric functions 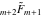 , or Stirling numbers , or Stirling numbers 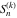 : :
|