|
For real values of the argument 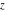 and nonnegative integer and nonnegative integer 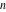 , the differentiated gamma functions , the differentiated gamma functions 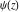 , , 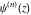 , , 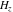 , and , and 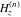 are real (or infinity). The function are real (or infinity). The function 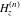 is real (or infinity) for real values of argument is real (or infinity) for real values of argument 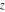 and integer and integer 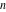 . .
The differentiated gamma functions 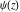 , , 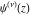 , , 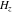 , and , and 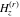 have simple values for zero arguments: have simple values for zero arguments:
The differentiated gamma functions 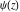 , , 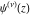 , , 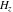 , and , and 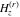 with rational arguments can sometimes be evaluated through classical constants and logarithms, for example: with rational arguments can sometimes be evaluated through classical constants and logarithms, for example:
The previous relations are particular cases of the following general formulas:
The differentiated gamma functions 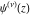 and and 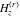 with integer parameters with integer parameters 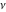 and and 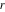 have the following representations: have the following representations:
The digamma function 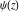 and the harmonic number and the harmonic number 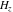 are defined for all complex values of the variable are defined for all complex values of the variable 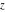 . The functions . The functions 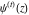 and and 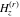 are analytical functions of are analytical functions of 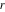 and and 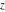 over the whole complex over the whole complex 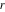 ‐ and ‐ and 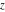 ‐planes. For fixed ‐planes. For fixed 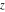 , the generalized harmonic number , the generalized harmonic number 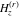 is an entire function of is an entire function of 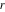 . .
The differentiated gamma functions 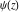 and and 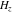 have an infinite set of singular points have an infinite set of singular points 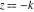 , where , where 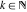 for for 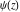 and and 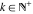 for for 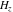 . These points are the simple poles with residues . These points are the simple poles with residues 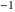 . The point . The point 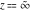 is the accumulation point of poles for the functions is the accumulation point of poles for the functions 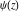 , , 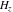 , and , and 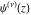 (with fixed nonnegative integer (with fixed nonnegative integer 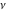 ), which means that ), which means that 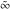 is an essential singular point. is an essential singular point.
For fixed nonnegative integer 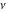 , the function , the function 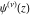 has an infinite set of singular points: has an infinite set of singular points: 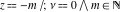 are the simple poles with residues are the simple poles with residues 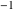 ; and ; and 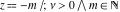 are the poles of order are the poles of order 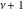 with residues with residues 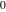 . .
For fixed 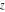 , the function , the function 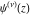 does not have poles and the function does not have poles and the function 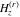 has only one singular point at has only one singular point at 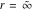 , which is an essential singular point. , which is an essential singular point.
The functions 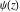 and and 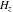 do not have branch points and branch cuts. do not have branch points and branch cuts.
For integer 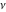 , the function , the function 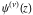 does not have branch points and branch cuts. does not have branch points and branch cuts.
For fixed noninteger 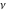 , the function , the function 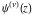 has two singular branch points has two singular branch points 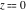 and and 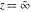 , and it is a single‐valued function on the , and it is a single‐valued function on the 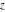 ‐plane cut along the interval ‐plane cut along the interval 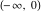 , where it is continuous from above: , where it is continuous from above:
For fixed 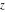 , the functions , the functions 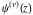 and and 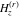 do not have branch points and branch cuts. do not have branch points and branch cuts.
The differentiated gamma functions 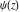 , , 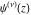 , , 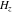 , and , and 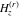 do not have periodicity. do not have periodicity.
The differentiated gamma functions 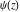 , , 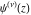 , , 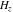 , and , and 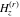 have mirror symmetry: have mirror symmetry:
The differentiated gamma functions 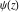 , , 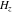 , and , and 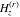 have the following series expansions near regular points: have the following series expansions near regular points:
Near singular points, the differentiated gamma functions 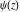 , , 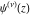 , , 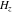 , and , and 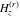 can be expanded through the following series: can be expanded through the following series:
Here 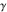 is the Euler gamma constant is the Euler gamma constant 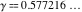 . .
Except for the generalized power series, there are other types of series through which differentiated gamma functions 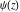 , , 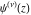 , , 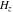 , and , and 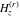 can be represented, for example: can be represented, for example:
The asymptotic behavior of the differentiated gamma functions 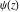 , , 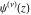 , , 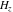 , and , and 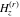 can be described by the following formulas (only the main terms of the asymptotic expansions are given): can be described by the following formulas (only the main terms of the asymptotic expansions are given):
The differentiated gamma functions 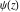 , , 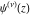 , , 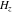 , and , and 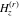 can also be represented through the following equivalent integrals: can also be represented through the following equivalent integrals:
The following formulas describe some of the transformations that change the differentiated gamma functions into themselves:
Transformations with arguments that are integer multiples take the following forms:
The following transformations represent summation theorems:
The differentiated gamma functions 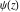 , , 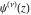 , , 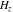 , and , and 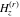 satisfy the following recurrence identities: satisfy the following recurrence identities:
The previous formulas can be generalized to the following recurrence identities with a jump of length 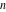 : :
The derivatives of the differentiated gamma functions 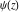 , , 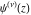 , , 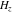 , and , and 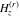 have rather simple representations: have rather simple representations:
The corresponding symbolic 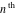 -order derivatives of all the differentiated gamma functions -order derivatives of all the differentiated gamma functions 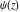 , , 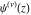 , , 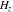 , and , and 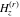 can be expressed by the following formulas: can be expressed by the following formulas:
|