|
The rounding and congruence functions have a long history that is closely related to the history of number theory. Many calculations use rounding of the floating-point and rational numbers to the closest smaller or larger integers. J. Nemorarius (1237) was one of the first mathematicians to use the quotient of two numbers 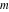 and and 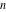 in a modern sense, but the word quotient appeared for the first time around 1250 in the writings of Meister Gernadus. in a modern sense, but the word quotient appeared for the first time around 1250 in the writings of Meister Gernadus.
Special notations for rounding and congruence functions were introduced much later. C. F. Gauss (1801) suggested the symbol mod (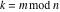 ) for the notation of the property that the ratio ) for the notation of the property that the ratio 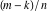 is an integer. He observed that is an integer. He observed that 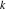 and and 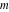 are the congruent modulo are the congruent modulo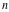 . The number . The number 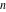 is called modulus. is called modulus.
C. F. Gauss (1808) and J. Liouville (1838) widely used the floor and round functions in their investigations. They and other mathematicians used different and sometimes confusing notations for those functions. The modern notations of 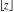 and and 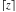 for floor and ceiling functions, respectively, were suggested by K. E. Iverson (1962). The notation for floor and ceiling functions, respectively, were suggested by K. E. Iverson (1962). The notation 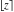 for the rounding function was proposed by J. Hastad (1988). for the rounding function was proposed by J. Hastad (1988).
|