|
The best-known properties and formulas of the Fibonacci and Lucas numbers
Simple values at zero and infinity
The Fibonacci and Lucas numbers  and and 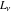 have the following values at zero and infinity: have the following values at zero and infinity:
Specific values for specialized variables
The Fibonacci and Lucas numbers  and and 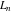 with integer argument with integer argument  can be represented by the following formulas: can be represented by the following formulas:
For the cases of integer arguments 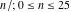 , the values of the Fibonacci and Lucas numbers , the values of the Fibonacci and Lucas numbers 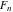 and and 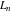 can be described by the following table: can be described by the following table:
Analyticity
The Fibonacci and Lucas numbers 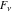 and and  are entire analytical functions of are entire analytical functions of 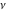 that are defined over the whole complex that are defined over the whole complex 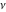 -plane: -plane:
Periodicity
The Fibonacci and Lucas numbers 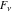 and and 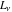 do not have periodicity. do not have periodicity.
Parity and symmetry
The Fibonacci and Lucas numbers 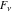 and and 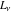 generically do not have parity, but they have mirror symmetry: generically do not have parity, but they have mirror symmetry:
Poles and essential singularities
The Fibonacci and Lucas numbers 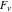 and and 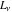 have only the singular point have only the singular point 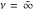 . It is an essential singular point. . It is an essential singular point.
Branch points and branch cuts
The Fibonacci and Lucas numbers 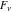 and and  do not have branch points and branch cuts over the complex do not have branch points and branch cuts over the complex 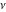 -plane. -plane.
Series representations
The Fibonacci and Lucas numbers 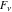 and and  have the following series expansions (which converge in the whole complex have the following series expansions (which converge in the whole complex 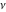 -plane): -plane):
Asymptotic series expansions
The asymptotic behavior of the Fibonacci and Lucas numbers  and and  is described by the following formulas: is described by the following formulas:
Other series representations
The Fibonacci and Lucas numbers 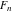 and and 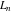 for integer nonnegative for integer nonnegative  can be represented through the following sums involving binomials: can be represented through the following sums involving binomials:
Integral representations
The Fibonacci and Lucas numbers  and and 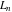 have the following integral representations on the real axis: have the following integral representations on the real axis:
Generating functions
The Fibonacci and Lucas numbers  and and 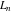 can be represented as the coefficients of the series of the corresponding generating functions: can be represented as the coefficients of the series of the corresponding generating functions:
Transformations: Addition formulas
The Fibonacci and Lucas numbers 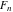 and and 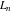 satisfy numerous addition formulas: satisfy numerous addition formulas:
Transformations: Multiple arguments
The Fibonacci and Lucas numbers 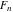 and and 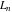 satisfy numerous identities, for example the following multiple argument formulas: satisfy numerous identities, for example the following multiple argument formulas:
Transformations: Products and powers of the direct function
The Fibonacci and Lucas numbers  and and 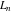 satisfy numerous identities for products and powers: satisfy numerous identities for products and powers:
Identities
The Fibonacci and Lucas numbers 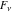 and and 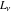 are solutions of the following simple difference equation with constant coefficients: are solutions of the following simple difference equation with constant coefficients:
The Fibonacci and Lucas numbers  and and 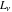 satisfy numerous recurrence identities: satisfy numerous recurrence identities:
Other identities for Fibonacci and Lucas numbers 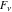 and and 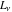 are just functional identities: are just functional identities:
Complex characteristics
The Fibonacci and Lucas numbers 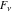 and and 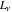 have the following complex characteristics for complex arguments: have the following complex characteristics for complex arguments:
Differentiation
The Fibonacci and Lucas numbers 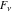 and and  have the following representations for derivatives of the first and have the following representations for derivatives of the first and 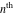 orders or the arbitrary fractional order orders or the arbitrary fractional order 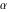 : :
Differential equations
The Fibonacci and Lucas numbers 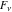 and and 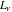 satisfy the following third-order linear differential equation: satisfy the following third-order linear differential equation:
where 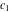 , , 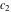 , and , and 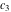 are arbitrary constants. are arbitrary constants.
Indefinite integration
Some indefinite integrals for Fibonacci and Lucas numbers 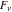 and and 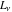 can be evaluated as follows: can be evaluated as follows:
Laplace transforms
Laplace transforms 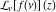 of the Fibonacci and Lucas numbers of the Fibonacci and Lucas numbers 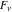 and and 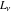 can be represented by the following formulas: can be represented by the following formulas:
Summation
There exist many formulas for finite summation of Fibonacci and Lucas numbers, for example:
Here are some corresponding infinite sums:
And here are some multiple sums:
Limit operation
Some formulas including limit operations with Fibonacci and Lucas numbers 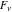 and and 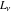 take on symmetrical forms: take on symmetrical forms:
Other identities
The Fibonacci numbers 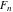 can be obtained from the evaluation of some determinates, for example: can be obtained from the evaluation of some determinates, for example:
|